Rybníček Kaprníček
Růst a jeho meze
Věnuji své dobré, milé a sympatické studentce Petře Rybníčkové
Milí čtenáři, mám radost, že Vás mohu už po čtvrté uvítat v pohádkovém lese [3], [4], [5]. Nepochybuji o tom, že už se těšíte na setkání s krásnou a sympatickou princeznou Alguelitou[1] i s vílami a kovílasy[2]. Čtenář, který není v našem pohádkovém lese ponejprv, už ví, že krásná a vzdělaná Alguelita, matematicky erudovaná zooložka a ekoložka, se svým tradičním pohádkovým kolegyním - princeznám podobá svými krásnými dlouhými kaštanovými vlasy, velkýma dobro vyzařujícíma očima, milým úsměvem, cudností a skromností, avšak odmítá nepraktické princeznovské šaty a nosívá vždy kalhoty, k nim zpravidla tričko, tentokrát měla zas své oblíbené hnědé džíny a zelené tričko se základními rovnicemi termodynamiky, kvantové mechaniky a speciální teorie relativity[3]. Je svým založením intelektuálka, velice inteligentní a velice laskavá.
A jako já coby autor vítám v pohádce vás, čtenáře, tak princezna Alguelita uvítala v pohádkovém lese skupinu poznáníchtivých studentů kvarty z nejbližšího osmiletého gymnázia, aby byli svědky počátku historie pohádkolesního rybníčku Kaprníčku. (V pohádce to jde, aby se rybníček najednou objevil.) A přivítala i některé své blízké přátele: víly Rychlici a Eskřivku a kovílase Pomalíka.
Dětem se svěřila se záměrem oživit rybníček Kaprníček rybami. Ty hned přišly s nápadem, že by to měly být zlaté rybky. Alguelita si vážila jejich iniciativy, nicméně zlaté rybičky v Kaprníčku se jí nezamlouvaly. Ony sice stejně nejsou zlaté, nýbrž červené (což je ovšem klamání veřejnosti), ale hlavně nechtěla, aby cokoli v pohádkovém lese připomínalo pošetilou lidskou honbu za materiálním bohatstvím, jedním z jehož symbolů je zlato, a s ním i přídavné jméno "zlatý". A tak, jak už i jméno rybníčka naznačuje, bude patřit především kapříkům. Na začátku tam několik párů nasadila a v duchu jim slíbila co nejlepší podmínky, aby se jim tam dobře vedlo a spokojeně se rozmnožovali.
Jak se bude množství kapříků v čase měnit? Přirozeně, čím více kapříků tam bude, tím více bude mezi nimi potenciálních rybích maminek a tatíků, a tedy tím více jich za jednotku času přibude. Alguelita dětem řekla, že tuto závislost můžeme vyjádřit základní homogenní růstovou rovnicí
y' = a.y,
kde y označuje množství kapříků v daném čase a y' je tzv. derivace veličiny y podle času, tedy y' vyjadřuje jak rychle zrovna množství kapříků roste. Čím více jich je, tím více jich přibývá. Jejich "fertilitu" vyjadřuje konstanta úměrnosti a. Pro rychleji přibývající druhy má a větší hodnotu. - Děti poslouchaly a na tváři jedné z nich, Markéty Moudré, se začal objevovat jakýsi výraz pochybností či nesouhlasu. Alguelitě to neušlo a zeptala se jí, co že se jí nelíbí. Markéta vysvětlila, že takový postup přece můžeme použít jen na spojité veličiny, které se mohou měnit i libovolně málo, kdežto počet rybiček je vyjádřen přirozeným číslem, a proto se neomezeně málo měnit nemůže, nejmenší možná změna je o 1. Alguelita jí odpověděla:
"Máš pravdu, Markéto (čtenář si může vybrat, zda pohádková princezna nějakým pohádkovým způsobem mohla poznat jména svých hostů, či zda děti při vstupu do pohádky uplatnily dobrý, u nás ve školách ovšem zcela opomíjený zvyk mít na sobě jmenovku). Když máme velký počet jedinců, tak ta změna o 1 je relativně tak malá, že i ten jejich přirozenočíselný počet můžeme považovat za spojitou veličinu. Pro nás však je na místě jiná úvaha. Ty mluvíš o počtu kapříků, já jsem mluvila o množství. A to nemusíme vyjadřovat pomocí počtu jedinců, nýbrž třeba pomocí jejich celkové hmotnosti, a to už spojitá veličina je. Vzpomínám si, že když jsem před lety studovala, můj učitel matematiky výklad o diferenciálních rovnicích začínával podobným příkladem, a pro celkovou hmotnost rybiček zavedl pojem ichthyomasa[4], a tak my při vyjadřování množství kapříků mějme na mysli jejich ichthyomasu; y tedy vyjadřuje ji. Ta diferenciální rovnice pro růst ichthyomasy je určitou idealizací, život je složitý, ale k popisu vývoje kapří populace nám docela vyhovuje.
Aby se kapříci řádně množili, musejí mít zajištěny dobré podmínky k životu. A to je na mně, na vílách a kovílasech, abychom je zajistili. Děti, co myslíte, dokážeme to?"
Tváře dětí vyjadřovaly souhlas. A tak se princezna opět ujala slova:
"Až budete znát více z matematiky, dovíte se, že řešením základní homogenní růstové rovnice je každá exponenciální funkce tvaru
y = C.eat.
Zde ponejprv používáme symbol t pro čas. On ve skutečnosti je už obsažen v základní homogenní růstové rovnici kde y' označuje derivaci podle času, tedy to, jak se ichthyomasa mění v závislosti na čase. A konstanta C vyjadřuje počáteční velikost ichthyomasy; když dosadíme t = 0 (víme, že jakékoli číslo umocněno na nultou je 1) dostaneme y = C."
Nedůvěřivá Markéta zas naznačila, že má co říci. "Vždyť ale to ichthyomasa poroste nade všechny meze! Odněkdy se kapříci do rybníčka nevejdou!"
Alguelita poznamenala, že v pohádce by sice rybníček mohl růst podle potřeby kapříků, nicméně tím by se pohádka zpronevěřila svému poslání ukázat lidem svět sice jiný, než ten jejich, ale takový, který by je motivoval k žádoucí změně způsobu života, myšlení a jednání. A k tomu potřebujeme nezvětšující se rybníček. Oni ti lidé na tom svém omezeném světě si počínají tak, jako by se zvětšoval úměrně jejich náročnosti. Neberou v úvahu zákony přírody. V pohádce nesmíme tuto jejich hloupost podporovat. Vážíme si přírody - se všemi jejími zákony. - Markétina námitka tím ovšem nebyla vyřešena.
V myslích dětí se rodil nápad, co kdyby se tedy pro potřeby pohádky vymyslel jiný, třeba méně přirozený, zákon růstu ichthyomasy kapříků, ale takový, že by respektoval konečnost Kaprníčku.
A to už tu byl připraven kovílas Pomalík, který dětem předložil nápad, co kdyby se pro potřeby pohádkového lesa kapřící rozmnožovali pomocí 0,5-zpomalené růstové rovnice
y' = a.y0,5,
tedy časová derivace y' ichthyomasy y by zde nebyla přímo úměrná ichthyomase y, nýbrž jen její druhé odmocnině. A kovílas Pomalík ještě dodal, že zde růst podle takové rovnice by opravdu byl poněkud nepřirozený a ani smysl konstanty a není tak zřetelný jako v případě základní homogenní růstové rovnice.[5] A dodal, že za těchto okolností stojí za to si život zjednodušit tím, že položíme a = 1, tedy
y' = y0,5.
Vědunka Rybníčková trochu zaprotestovala, že taková rovnice je v nepořádku, neboť na levé straně máme údaj s rozměrem ichthyomasa za čas a na pravé straně je rozměr odmocnina z ichthyomasy. Kovílas jí vysvětlil, že probíráme zjednodušený příklad a pro něj si představujeme, že máme jednotky pevně zvoleny tak, aby rovnice platila[6]. Většina dětí tomu sice nerozuměla, ale ono to vlastně nevadilo. Zjednodušení vede k větší názornosti.
A záhy Pomalík své posluchače seznámil i s řešením této diferenciální rovnice:
y = (t/2 + C)2,
a vysvětlil, že zde počáteční množství kapříků nevyjadřuje přímo konstanta C, nýbrž její druhá mocnina.
Teď se ozval Jarda Jelínek, že to je kvadratická funkce, která sice neroste tak rychle jako exponenciála, ale jednou rybníček stejně nebude stačit.
Kovílas Pomalík se usmál a řekl, dobrá, nechť tedy přírůstek je konstantní, samozřejmě kladný:
y' = k
Tu se Vědomil Čísílko, který měl už prostudovány úvodní učebnice diferenciálního a integrálního počtu, neudržel a zvolal: "Vždyť tohle je triviální úloha na výpočet integrálu!" Musí platit
y = kt + C.
To je ale přece lineární funkce!"
A k tomu Markéta Moudrá smutně dodala: "Ale takhle to také nepůjde. Vždyť tahle funkce také roste nade všechny meze, a tak jednou by byl kapříkům rybníček malý!"
Pomalík se usmál pod fousy a navrhl, že by se růst mohl zpomalovat, třeba tak, že by vývoj kapří populace byl popsán zpomalovací rovnicí
y' = a/y.
A hned děti seznámil s jejím řešením:
y = (2t + C)1/2,
kde C vyjadřuje druhou mocninu počáteční ichthyomasy.
Markétu Moudrou tentokrát s vyjádřením zklamání předběhla Vědunka Rybníčková: "Ona ta funkce roste zas nade všechny meze, i když ještě pomaleji než ta předchozí lineární. Má to vůbec naději? ... Ale víte, co by mě zajímalo? Co kdyby ten růst byl rychlejší než odpovídá základní homogenní růstové rovnicí?"
Princezně Algulitě se Vědunčina zvídavost velice zalíbila a o odpověď požádala, pochopitelně, vílu Rychlici. Ta se hned s elánem ujala slova. "Děti, víte, kdybychom to dělali moc obecně, tak vy z toho budete jeleni a já se třeba také zamotám - a bude ze mne laň. Ani víla totiž není neomylná. A tak si vyberme kvadraticky zrychlenou růstovou rovnici
y' = a.y2.
Přidávám se k Pomalíkovu názoru, že je rozumné položit a = 1. Máme tedy
y' = y2.
Hned vám uvedu řešení a doufám při tom, že se moc těšíte, až budete diferenciální rovnice řešit samy.
Řešení tedy je
y = 1/(C - t),
kde pro změnu konstanta C vyjadřuje převrácenou hodnotu počáteční hodnoty y."
Markéta radostně vykřikla: "Tahle funkce pro velké hodnoty t nejde k nekonečnu, to je skvělé ..., ale vlastně divné, vždyť by měla popisovat rychlejší růst než ty předchozí. A přitom ona dokonce míří k nule, tedy kapříci nám vyhynou"
Rychlice ji potvrdila, že takový růst by rozhodně kapříkům nesvědčil, ale z jiného důvodu. Připomněla, že ve jmenovateli nesmí být 0, tedy t se nesmí rovnat C. Na počátku, při t = 0, byla ichthyomasa v rybníčku 1/C. Růst ichthyomasy, v tomto speciálním případě vyjádřený lineární lomenou funkcí, může probíhat jen v době, kdy t < 1/C; roste nade všechny meze dokonce už v konečném čase[7], blížícím se hodnotě 1/C. Je tedy samozřejmě také neslučitelný s možnosmi rybníčku Kaprníčku.
Mají kapříci vůbec nějakou naději na trvale udržitelný život v Kaprníčku? Alguelita viděla dětem na tvářích, že jim tato otázka leží v jejich dosud deformovanou ekonomikou nezatížených myslích. Protože se těšila, že na závěr něco zajímavého poví a nechtěla mít dlouhý monolog, dala slovo víle Eskřivce.
Ta mysli svých milých posluchačů vrátila k první rovnici, k té, již jsme nazvali základní homogenní růstovou rovnicí. A řekla, že dokud je v rybníčku místa dost, tak nám rovnice funguje. Ale jakmile se množství ichthyomasy začne přibližovat jakési nepřekročitelné hranici (říkáme jí suprémum a označíme ji U), tak se v důsledku měnících se podmínek fertilita rybiček bude zmenšovat. Jednoduše to matematicky můžeme modelovat tak, že konstantu úměrnosti a nahradíme jakýmsi koeficientem, který se zpočátku od a téměř nebude lišit, ale jak se y bude blížit suprému, koeficient se bude zmenšovat a blížit k nule. Nahraďme tedy v základní homogenní růstové rovnicí konstantu a koeficientem a.(1 - y/U). Dostaneme tak logistickou rovnici
y' = a.(1 - y/U).y,
jejímž řešením je tzv. logistická funkce
y = U / (1 + B e-at).
Grafem logistické funkce je tzv. logistická křivka, o níž si ještě něco povědí. Konstanta B opět souvisí s počátečním stavem. Jestliže počáteční množství ichthyomasy označíme y0, platí:
B = U/y0 - 1.
Vyjádření logistické funkce můžeme upravit tak, aby se v něm počáteční hodnota y0 přímo vyskytovala:
y = U y0 / (y0 + (U - y0) e-at)
Hodnoty logistické funkce nikdy nepřekročí U, roste-li t nade všechny meze, tak se její hodnoty hodnotě U blíží.
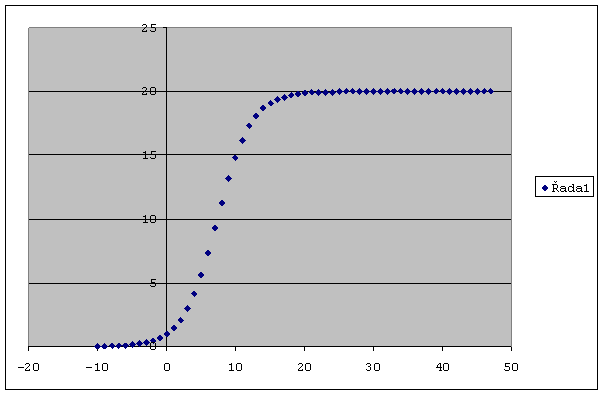
Historie kapříků začala v čase t = 0. Do rovnice pro logistickou funkci můžeme ovšem formálně dosazovat i záporné hodnoty času t. Logistická křivka zakreslená pro všechny reálné hodnoty času t (tedy i pro t < 0) má tvar naznačený na obrázku (zde je U = 20, y0 = 1, a = 0,4). Protože svým tvarem připomíná (aspoň těm, kdo mají určitou fantasii) písmeno S, patří mezi tzv. S-křivky (při tom se víla nápadně usmála). S-křivky jsou středově symetrické, druhá souřadnice středu souměrnosti musí být U/2, obecné vyjádření první souřadnice je složitější: a-1.ln(U/y0 - 1). V našem případě tedy je střed souměrnosti křivky bod [2,5.ln(19); 10] = [7,4; 10]. Logistická funkce je všude rostoucí, a když uvažujeme celý její definiční obor (množinu všech reálných čísel), je jejím oborem hodnot otevřený interval (0, U). Pro malé hodnoty argumentu se podobá funkci exponenciální, ale pak se růst začne zpomalovat. Protože Eskřivka si uvědomila, že už povídá dost dlouho, pro bližší porovnání exponenciální a logistické funkce odkázala děti na 19. svazek sborníku Mundus Symbolicus [6], aniž by si dělala neději, že tam děti pro poučení půjdou, a své vystoupení ukončila uspokojujícím sdělením, že našli, co hledali.
Vědunka Rybníčková se však rozhodně uspokojeně netvářila. Poprosila o slovo a připomněla, že k logistické funkci dospěli z předpokladu, že fertilita kapříků s ubýváním životního prostoru klesá, což však znamená, že se jim už nepovede tak dobře jako na začátku. Alguelita Vědunku pochválila za velice moudrou myšlenku a ujala se slova:
"Život bez změny není možný, a k tomu jsme jak vy lidé z reálného světa, tak i my z pohádky vybaveni schopností myslet, aby vše nebylo ponecháno náhodě. Kapříkům od určité zaplněnosti rybníčka bude těsno. Jestliže jim rybáři tím, že některé vyloví, pomohou zachovat životní prostor, prospějí tím kapří populaci, či jí ublíží? Snad se shodneme na tom, že prospějí, samozřejmě za předpokladu, že si počínají citlivě a uvážlivě. Takové vnější zásahy jsou oprávněné, pokud přírodě pomohou; rozhodně jí nesmějí ublížit. A když si lidé na takovém kapříkovi pochutnají - to není nic špatného. Ale pamatujte, přírodě se nesmí ubližovat. Člověk má přírodě sloužit k dobrému, svým způsobem dotvářet krásné Stvořitelovo dílo. Kdo se zabývá krajinou, tak o důležitosti spolupráce člověka a přírody nepochybuje.
Vraťme se však ke kapříkům. Ti ulovení mohou mít jiný názor než jaký je názor celku či vnějšího pozorovatele. Být kořistí, byť takového speciálního predátora, jakým je člověk, asi žádná radost není. - Teď si samozřejmě můžeme položit otázku, zda vůbec kapříci mohou mít názor či prožívat radost. Nechám ji nezodpovězenu. Problém s prostorem, který mají kapříci v Kaprničku, totiž máte i vy lidé na krásné a bohaté planetě Zemi. Přibývá vás, i když se to netýká všech národů. Jenže národy, které se nijak výrazně nerozmnožují, tak zas spotřebovávají stále více z bohatství, které je určeno všem, a nejen v současnosti, nýbrž i v budoucnosti. A tak svým způsobem všichni se podílíte na tom, že Země je stále těsnější a těsnější.
Neomezený růst není možný. Blízko mezní hodnoty by asi život moc radostný nebyl. Co s tím? On by to neměl zas být takový problém, jen umět použít rozum. Lidé o mezích vědí. A také vědí, že jedni druhé potřebují, že jsou navzájem na sobě závislí. Krásně to vyjadřuje název zprávy, kterou v poslední šestině dvacátého století vydala se svými spolupracovníky tehdejší norská ministerská předsedkyně Gro Harlem Brundtlandová: Naše společná budoucnost. Budoucnost není v konkurenci, nýbrž ve spolupráci. Budoucnost není v kontraproduktivním sobectví, nýbrž je ve schopnosti sdílet s druhými dobré i zlé. Budoucnost není v penězích, nýbrž je ve schopnosti umět se radovat - z druhých lidí, z přírody, ze zázraku života.
Je nám zde spolu dobře - aspoň pevně doufám, že jste rády u našeho Kaprníčku se mnou, s vílami i s kovílasem. Jsme spolu, povídáme si, a vůbec nevadí, že k tomu nemáme žádnou hostinu. Hezký a smysluplný život není v tom hodně mít, nýbrž v tom být plně člověkem a své tělesné i duševní schopnosti užívat ve prospěch dobra. Angažovat se pro druhé lidi, angažovat se pro přírodu.
Lidské sobectví a honba za penězi zaclonila lidem pohled k pravým životním hodnotám. Moc vám, milé děti, přeji, aby se vám rozjasnil výhled směrem k dobru, pravdě, lásce, spravedlnosti, směrem k plnosti života."
Vědunka Rybníčková krásné, moudré a vzdělané princezně Alguelitě, vílám Rychlici a Eskřivce i kovílasu Pomalíkoví jménem všech dětí poděkovala a všechny přátele z pohádky ujistila, že se budou snažit do svého myšlení i konání promítat to, co se u Kaprníčku dověděly. A Alguelita poděkovala vílám a kovílasovi za spolupráci, dětem za aktivní pozornost a vyjádřila naději na další setkání. Rozloučili se naplněni všichni pocitem dobré pohody a radosti z příjemně a užitečně strávené chvíle.
Literatura
1. Brundtlandová, Gro Harlem: Naše společná budoucnost. Praha, Academia 1991 (Originál Our Common Future, 1987)
2. Nečas, J.: Hrnečku, vař aneb Separace proměnných v české pohádce. Mundus Symbolicus 16(2008).
3. Nečas, J.: Vlci a zajíci v pohádkovém lese. Envigogika 2009/IV/2 (Inspirace) - Mundus Symbolicus 17 (2009).
4. Nečas, J.: Princezna Alguelita a rozmanitost v přírodě. Envigogika 2011/VI/1 (Inspirace)
5. Nečas, J.: Jeskyně Třináctka. Mundus Symbolicus 19 (2011)
6. Nečas, J.: Exponenciální a logistický růst. Mundus Symbolicus 19 (2011).
7. Elizagaray, Alga Marina: Niňos, Autores y Libros. La Habana, Gente Nueva 1981.
Praha, březen 2012
(Psáno pro Envigogiku a Mundus Symbolicus)
[1] Princezna je představena v [4] a [5], v [3] vystupuje princezna bez jména. Princeznino jméno, inspirované jménem autorky knihy [7], poukazující na možnosti pohádky pro sdělování důležitých, někdy obtížně vyjádřitelných skutečností, zdůrazňuje důležitost řas pro globální ekosystém; alga je latinsky a španělsky řasa; španělsky tvořená dvojnásobná zdrobnělina příponou -uelita je Algüelita, do češtiny přepisujeme česky foneticky Alguelita.
[2] Mužská obdoba víly. Český slovní základ víl je doplněn předponou ko- s obdobným významem jako u goniometrických funkcí a příponou -as, která je převzata z litevštiny jako základní příznak maskulina (tam jde o nominativní pádovou koncovku).
[3] F = E - TS, E = mc2, E = hf; viz [3].
[4] Úvod do diferenciálních rovnic ob semestr připadl do předvánočního období, kdy zmíněný Alguelitin učitel rád studentkám a studentům připomínal, jak se stala ryba křesťanským symbolem, a tedy i symbolem vánoc. Řecky ryba se řekne ιχθυς (ichthys), což se dá chápat jako zkratka vyznání "Iesus Christos, Theu Yios, Sōtēr", tedy "Ježíš Kristus, Syn Boží, Spasitel"). Kvůli připomenutí tohoto prvokřesanského vyznání přepisuji řecké θ poněkud archaicky "th", ač dnes běžně se už přepisuje jen "t".
[5] Nelineární diferenciální rovnice y' = yr, kde r ≠ 1, nejsou v souladu s obecně přijímaným proncipem superpozice.
[6] Rozměrově nekonzistentní, a tedy vyžadující pro daný problém vhodně pevně zvolenou soustavu jednotek, jsou i další rovnice diskutované Pomalíkem a Rychlicí; kdybychom trvali na rozměrové konzistenci, byly by příslošné rovnice velice nepřehledné a těžkopádné.
[7] Mechanické dosazení t > 1/C by vedlo k záporným hodnotám ichthyomasy y; řešení je smysluplné jen pro t < 1/C; vzhledem k zadání se tako omezujeme jen na hodnoty t z intervalu <0, 1/C)